RNA

Repository for RNA.

View the Project on GitHub Sirivasv/RNA

RNA (Rhythm-Note Alignment)

This is the description page for RNA, a symbolic music similarity measure using a modified version of local alignment. RNA uses a substitution function which consider the pitch class and the difference in the onset for each possible match. We also present a comparison made with these other similarity measures:

Based on the work by Janssen, et. al. (2015) and Janssen, et. al. (2017). We use the same MTC-ANN dataset, version 2.0.1, available here, the pieces were preprocessed just to change the extension to musicxml files.

The following sections describe the experiments and link to the code used on each one.

How it works?

Introduction

RNA comes from the intuiton that simple features such as pitch and duration can be of great use in analysis tasks like music similarity evaluations. It was first proposed to use the difference of start times of the notes as it is one of the most overlooked features on early similarity and distance measures tested. Also the penalizations for not matching strictly on the same pitch was worth of questioning if a more loose condition could improve the results. For this purpose the pitch matching is done using only the pitch class regardless on the octave. Now, just considering the amount of shared atomic elements like the ones described lack the judging of the more abstract structures present in music like the order in the melody, chords, motifs, etc. To tackle this issue an existing sequence matching algorithm was considered to modify and include the evaluation of the features described previously. The algorithm with the appropiate customization options that was selected is Local Alignment by considering its capabilites to consider relative order in the search of the longest common.

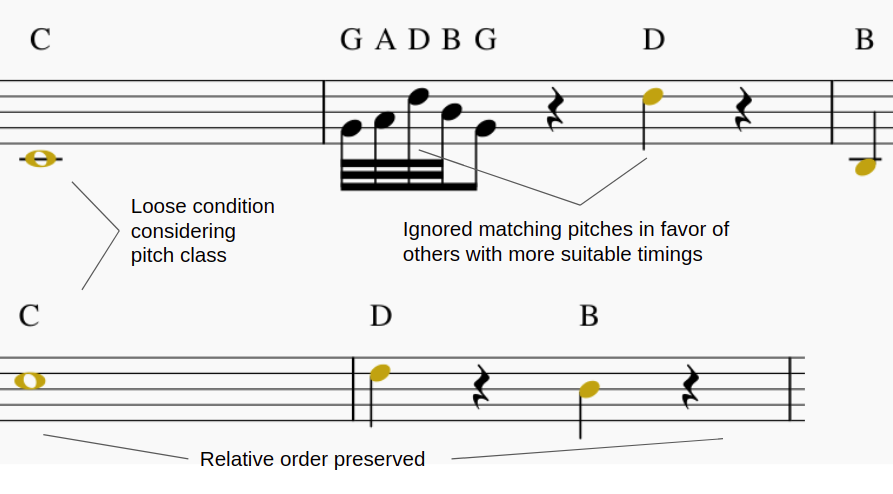
Image

To give a final score we can define it as the relation between the length of the Longest Common Subsequence (LCS) and the length of the longest melody from the two compared melodies A and B. To this effect, the RNA between melodies A and B is calculated as follows:

\[RNA(\mathbf{A},\mathbf{B}) = 1 - \frac{|LCS_{\mathbf{A},\mathbf{B}}|}{\max{(|\mathbf{A}|,|\mathbf{B}|)}}\]

To calculate the LCS between both melodies, we first need to eliminate their octave dependence, that is to say, notes are extracted regardless of the octave or the MIDI height in which they are located. Meaning, this representation takes all C notes as being of the same class, even though a C in the 3rd octave is lower than a C in the 5th octave. This is because, usually, only the relative distance with respect to the scale is taken into account when constructing chords and progression, and not their absolute distance in semitones.

Given two melodies A and B represented as a note class sequence, the LCS of notes can be calculated using the following recursive function:

\[\begin{split} &LCS(i,j) = \\ &\begin{cases} 0, \text{if } (i=0) \text{ or } (j=0) \\ \max{(LCS(i - 1,j), LCS(i,j - 1), LCS(i - 1,j - 1) + subs(i, j))}, \\ ~~~~~~\text{otherwise} \\ \end{cases} \end{split}\]

where subs, is defined as:

\[\begin{split} &subs(i,j) = \\ &\begin{cases} 1, \\ ~~~~~~\text{if } (\mathbf{A}[i] = \mathbf{B}[j]) \text{ and }\\ ~~~~~~~~~~(\mathbf{P}_{A}[i] - \mathbf{P}_{B}[j]) < (\mathbf{P}_{A}[i] + \mathbf{P}_{B}[j]) / C_E\\ 0, otherwise \\ \end{cases} \end{split}\]

where PA and PB are vectors calculated as:

\[\begin{split} \mathbf{P}_{A}[i] = start(\mathbf{A}[i]) - start(\mathbf{A}[i-1]) \\ \mathbf{P}_{B}[j] = start(\mathbf{B}[j]) - start(\mathbf{B}[j-1]) \end{split}\]

where start returns the starting point of a given note; and, CE is a scaling coefficient, the value of which was experimentally obtained as half the average of a typical P vector; in this case, it has a value of 64. This was implemented in order to incorporate a threshold that could make the distiction of significant differences between the notes. In this case we calculate how much the difference should be in order to be noticeable for the algorithm. It wouldn’t be appropiate to define a fixed value because of how much different musical pieces could be, instead what is fixed is the scale related to the onset times of each song, with the hypothesis to being able to suit multiple melodic sets.

The cardinality of the LCSA,B factor in is inherently maximized when the LCS recursive function reaches a stop scenario (required similarly in the Local Alignment measure). To ensure this, the original call to the LCS function should be with i and j initialized as the lengths of A and B respectively.

Controlled Experiments

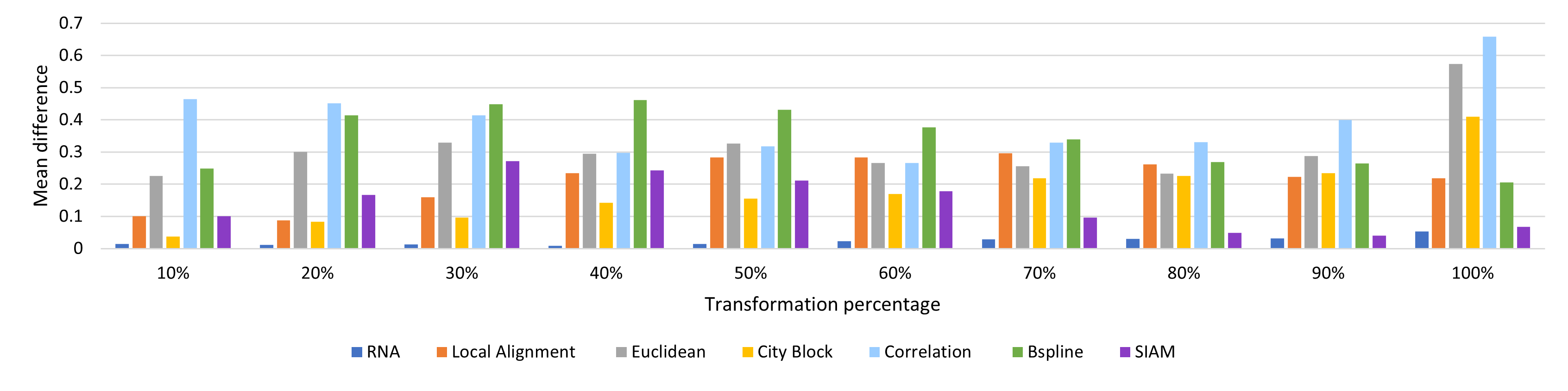
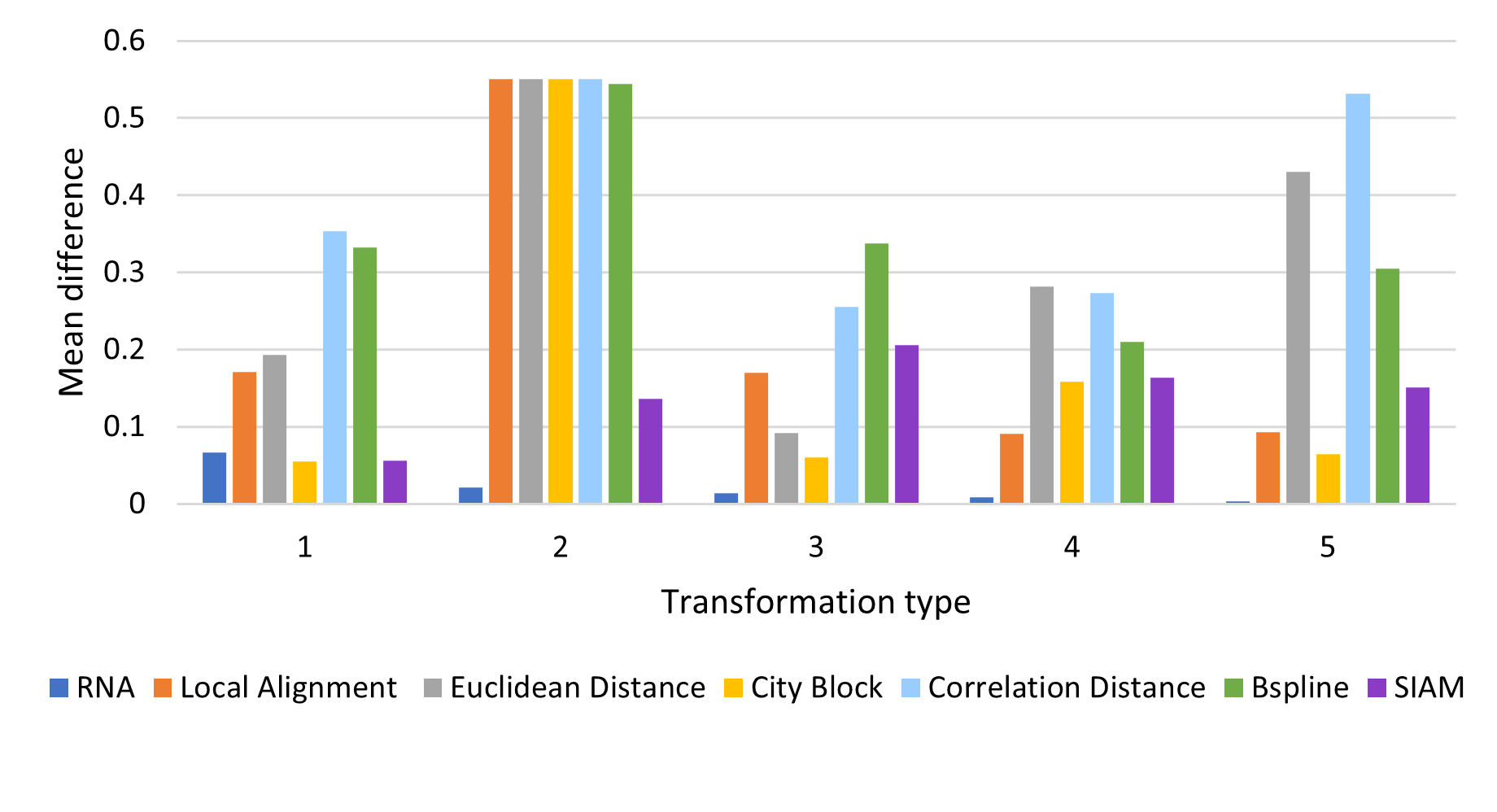
In these experiments a melody is modified with 4 types of modifications and by percentages (10, 20, …, 100). The expected value from each similarity measure after normalization should be equal to the percentage of the modification, for example a melody modified by 10% should have a distance of 0.1 with the original, and of 1.0 for a 100% modification.

The tested modifications made on the melody are:

The experiments were conducted using implementations based from Janssen and Urbano in the case of BSpline.

The corresponding Jupyter notebooks can be found in this respository following this link.

Results

Average Difference by percentage: Image

Average Difference by Modification Type: Image

Comparison with Expert annotations

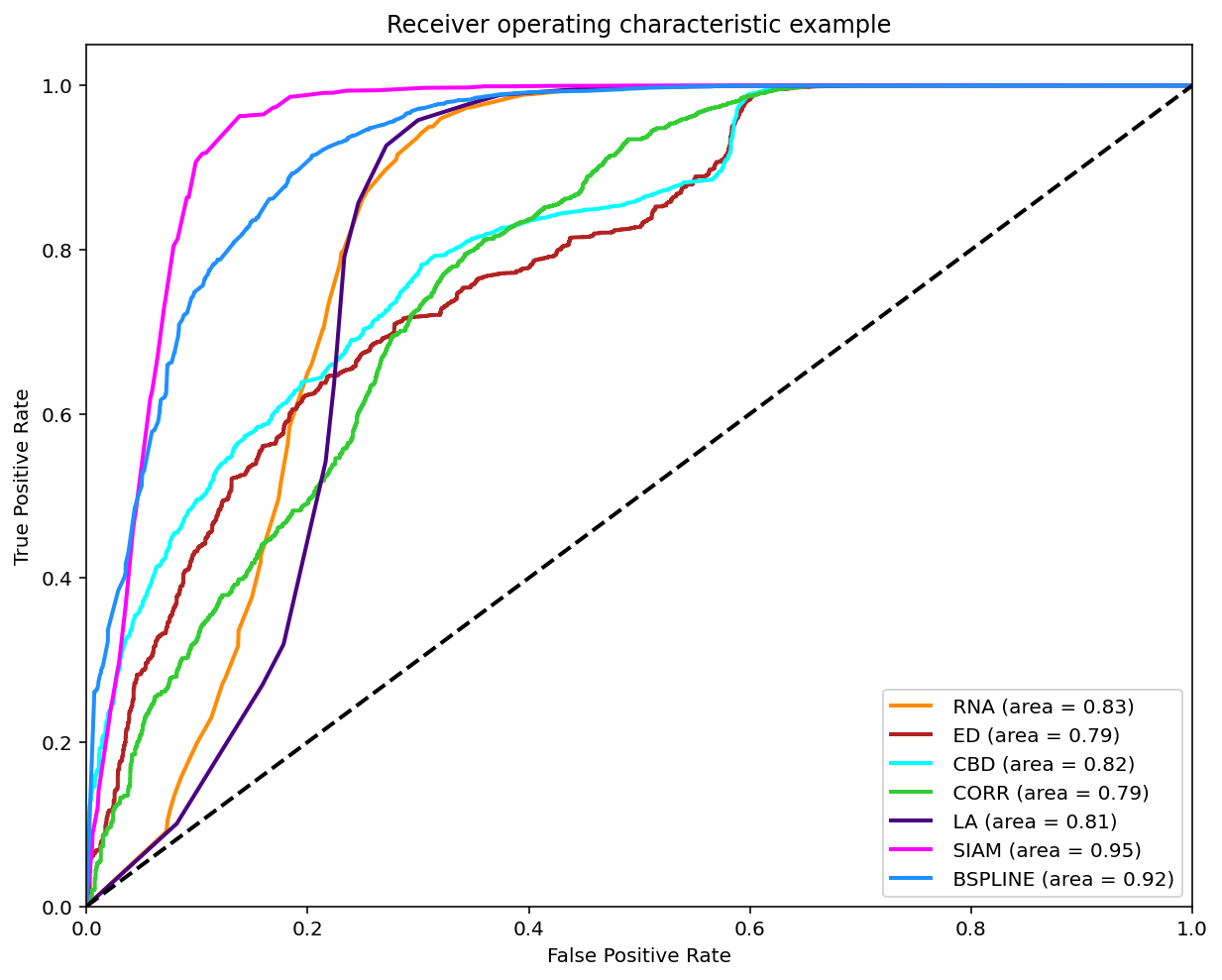
As reviewed in Janssen, et. al. (2017) a classification can be made on the matches found when comparing two melodies in order to compare it with the experts annotations by varying the threshold and ploting the ROC curve.

A modified version of this experiment was made, the main difference is using the similarity measures on all the possible comparissons annotated, that is compare each phrase of each tune to each other per tune family using all 7 similarity measures. The annotations are converted to 0 (identical), 0.5 (somewhat similar) and 1.0 (distinct). To make binary classifications we filtered and splited the data for 3 disctinct experiments. Each experiment took a pair to make the classification. The 3 possible pairs are: 0-0.5, 0.5-1 and 0-1. The reported graph is by taking the majority annotation, if no annotation has the majority the segment is not considered. And for further analysis the same experiments were replicated with filtered segments with an unanimity votes.

The corresponding Jupyter notebooks can be found in this respository following this link. The notebook with the results can be found here.

Results using Majority Vote

Classification (0-0.5)

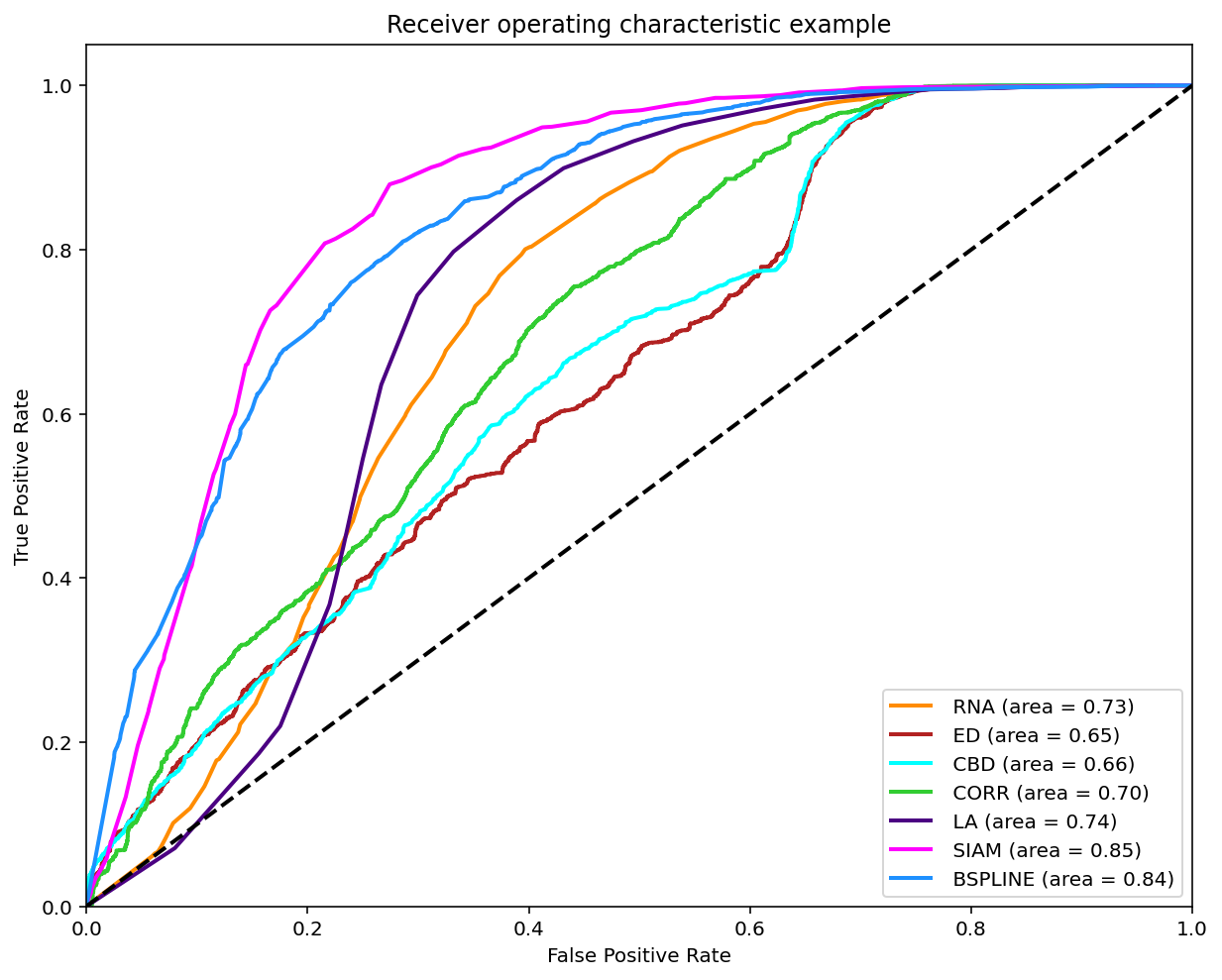
Image

Classification (0.5-1)

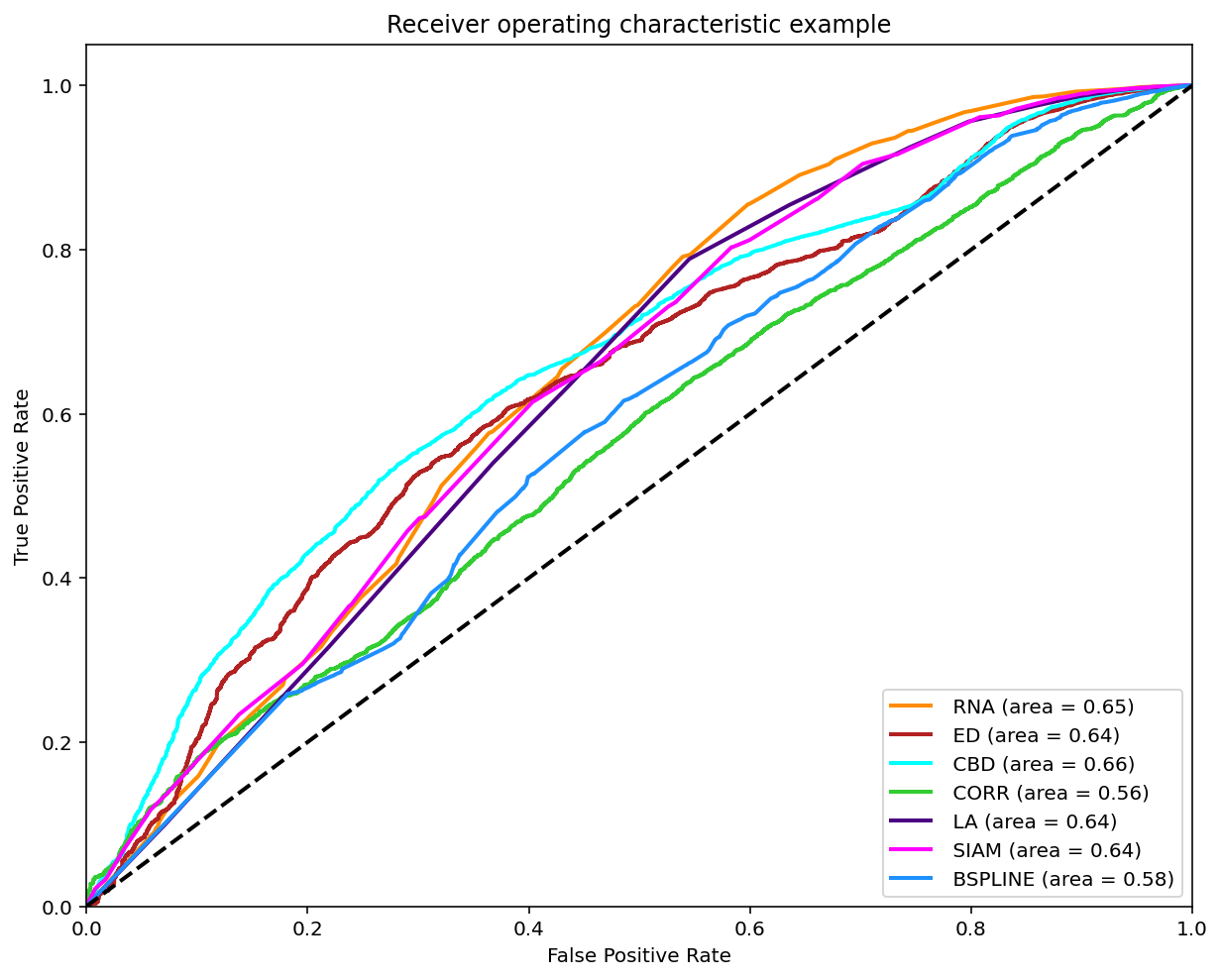
Image

Classification (0-1)

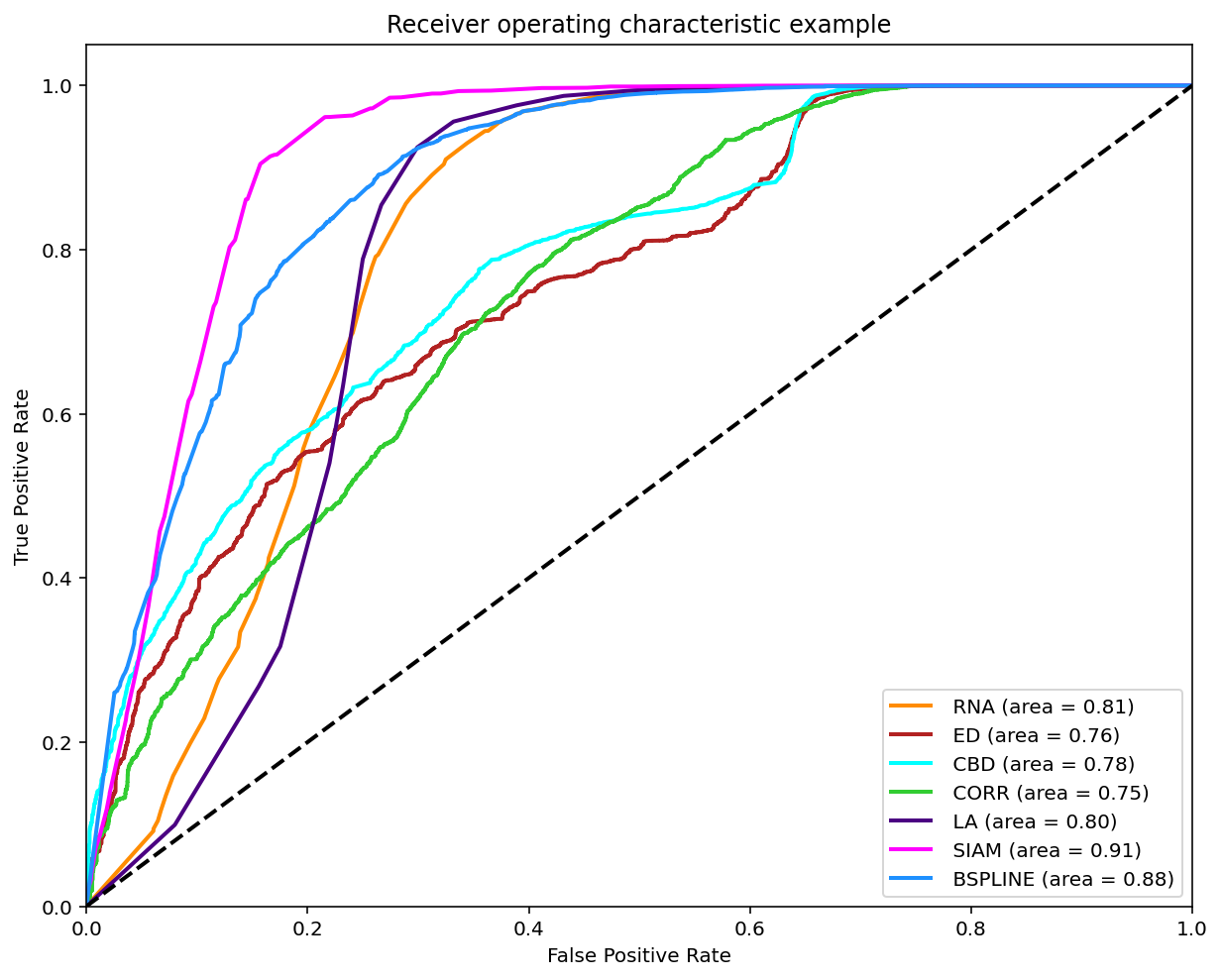
Image

Results using Unanimity Vote

Classification (0-0.5)

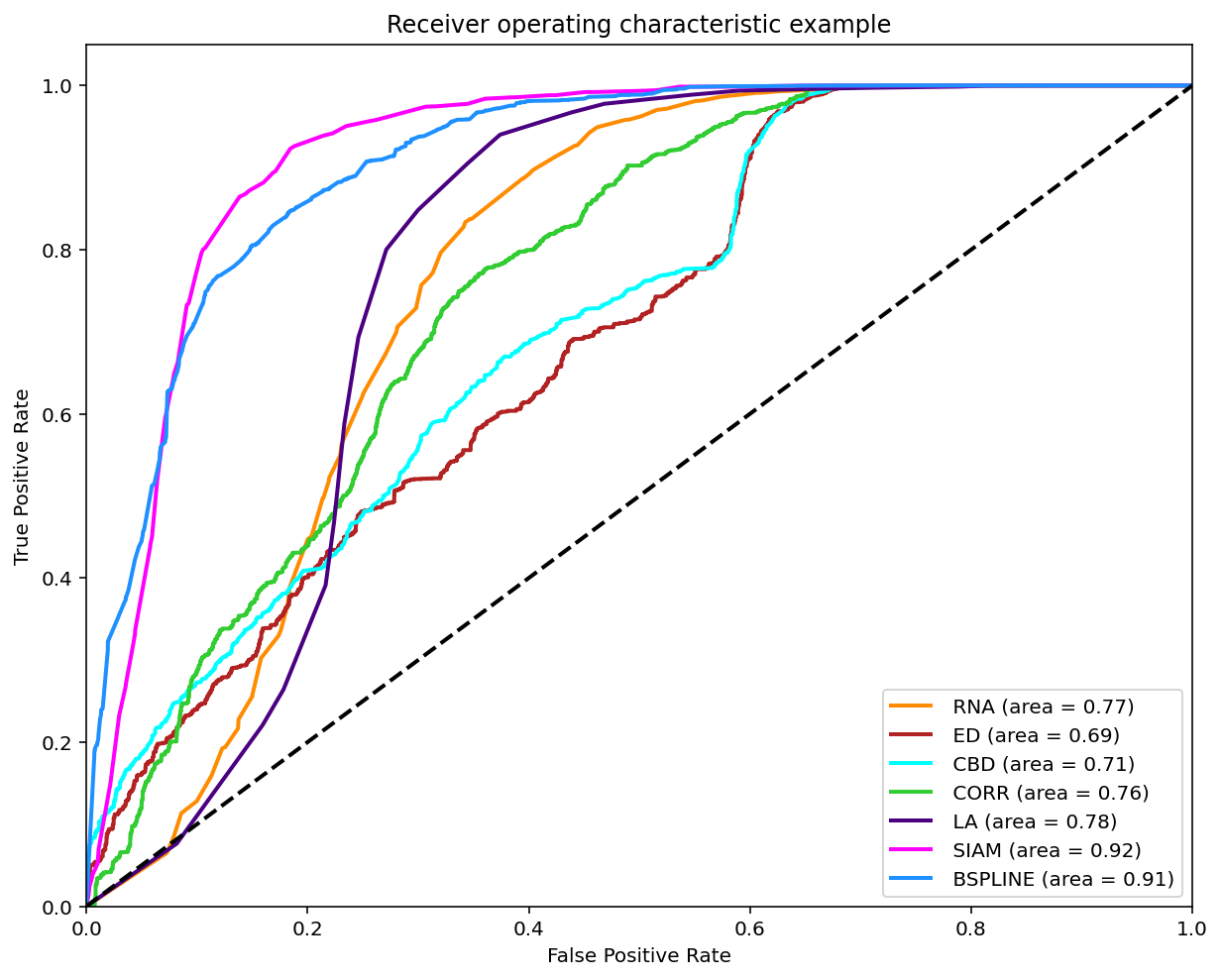
Image

Classification (0.5-1)

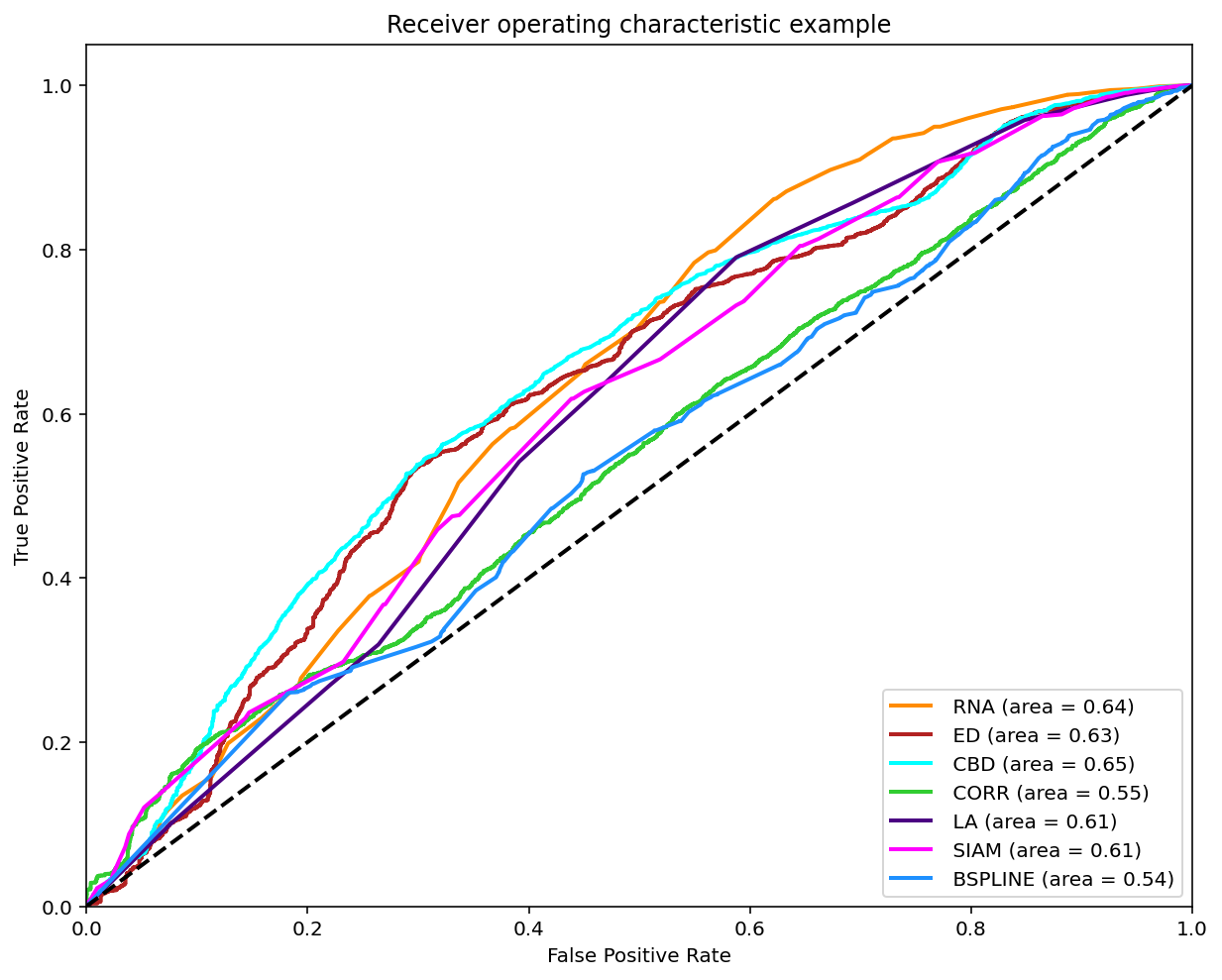
Image

Classification (0-1)

Image

Summary of F1 Scores

Majority Vote

Name 0 - 0.5 0.5 - 1 0 - 1
RNA_f1 0.7205 0.9309 0.9521
RNA_precision 0.5917 0.8765 0.9206
RNA_recall 0.9209 0.9926 0.9859
RNA_specificity 0.4633 0.1053 0.5406
ED_f1 0.6915 0.9281 0.9372
ED_precision 0.5339 0.8676 0.8863
ED_recall 0.9812 0.9976 0.9943
ED_specificity 0.2765 0.0263 0.3106
CBD_f1 0.6923 0.9288 0.9383
CBD_precision 0.5349 0.8686 0.8868
CBD_recall 0.9810 0.9979 0.9960
CBD_specificity 0.2795 0.0344 0.3132
CORR_f1 0.6984 0.9275 0.9355
CORR_precision 0.5510 0.8659 0.8829
CORR_recall 0.9536 0.9986 0.9947
CORR_specificity 0.3435 0.0109 0.2874
LA_f1 0.7462 0.9292 0.9552
LA_precision 0.6377 0.8702 0.9252
LA_recall 0.8992 0.9967 0.9873
LA_specificity 0.5685 0.0487 0.5685
SIAM_f1 0.7981 0.9299 0.9677
SIAM_precision 0.7304 0.8742 0.9510
SIAM_recall 0.8796 0.9932 0.9851
SIAM_specificity 0.7258 0.0855 0.7258
BSPLINE_f1 0.7588 0.9277 0.9512
BSPLINE_precision 0.6795 0.8655 0.9200
BSPLINE_recall 0.8590 0.9997 0.9846
BSPLINE_specificity 0.6577 0.0060 0.5375

Unanimity Vote

Name 0 - 0.5 0.5 - 1 0 - 1
RNA_f1 0.7048 0.9612 0.9689
RNA_precision 0.5605 0.9262 0.9498
RNA_recall 0.9493 0.9989 0.9887
RNA_specificity 0.5379 0.0297 0.6051
ED_f1 0.6509 0.9606 0.9581
ED_precision 0.4901 0.9242 0.9219
ED_recall 0.9686 1.0000 0.9973
ED_specificity 0.3745 0.0012 0.3613
CBD_f1 0.6519 0.9608 0.9590
CBD_precision 0.4889 0.9252 0.9228
CBD_recall 0.9779 0.9992 0.9983
CBD_specificity 0.3653 0.0163 0.3680
CORR_f1 0.6707 0.9606 0.9583
CORR_precision 0.5337 0.9241 0.9207
CORR_recall 0.9024 1.0000 0.9991
CORR_specificity 0.5105 0.0000 0.3490
LA_f1 0.7394 0.9607 0.9701
LA_precision 0.6094 0.9243 0.9523
LA_recall 0.9401 1.0000 0.9885
LA_specificity 0.6260 0.0028 0.6260
SIAM_f1 0.8315 0.9608 0.9815
SIAM_precision 0.7566 0.9249 0.9697
SIAM_recall 0.9229 0.9995 0.9936
SIAM_specificity 0.8157 0.0118 0.7651
BSPLINE_f1 0.7903 0.9606 0.9704
BSPLINE_precision 0.7410 0.9241 0.9527
BSPLINE_recall 0.8465 1.0000 0.9887
BSPLINE_specificity 0.8163 0.0000 0.6292

Summary of Best ROC Values (closest to tpr=1.0 and fpr=0.0)

Majority Vote

Name 0 - 0.5 0.5 - 1 0 - 1
RNA_best_roc_value 0.4037 0.2571 0.5856
RNA_best_roc_f1 0.7052 0.8778 0.9328
RNA_best_roc_precision 0.6302 0.9014 0.9359
RNA_best_roc_recall 0.8005 0.8553 0.9298
RNA_best_roc_specificity 0.6032 0.4017 0.6557
ED_best_roc_value 0.2656 0.2278 0.3704
ED_best_roc_f1 0.6897 0.6718 0.7569
ED_best_roc_precision 0.5390 0.9182 0.9278
ED_best_roc_recall 0.9574 0.5297 0.6392
ED_best_roc_specificity 0.3082 0.6981 0.7312
CBD_best_roc_value 0.2681 0.2565 0.4215
CBD_best_roc_f1 0.6900 0.6801 0.8490
CBD_best_roc_precision 0.5401 0.9244 0.9208
CBD_best_roc_recall 0.9549 0.5380 0.7877
CBD_best_roc_specificity 0.3132 0.7186 0.6338
CORR_best_roc_value 0.3141 0.0955 0.3737
CORR_best_roc_f1 0.6630 0.7153 0.8577
CORR_best_roc_precision 0.5915 0.8838 0.9092
CORR_best_roc_recall 0.7540 0.6007 0.8117
CORR_best_roc_specificity 0.5601 0.4948 0.5620
LA_best_roc_value 0.4712 0.2435 0.6254
LA_best_roc_f1 0.7413 0.8417 0.9340
LA_best_roc_precision 0.6513 0.9025 0.9435
LA_best_roc_recall 0.8602 0.7886 0.9247
LA_best_roc_specificity 0.6111 0.4549 0.7008
SIAM_best_roc_value 0.6054 0.2198 0.7474
SIAM_best_roc_f1 0.7981 0.8480 0.9397
SIAM_best_roc_precision 0.7304 0.8980 0.9674
SIAM_best_roc_recall 0.8796 0.8032 0.9136
SIAM_best_roc_specificity 0.7258 0.4166 0.8339
BSPLINE_best_roc_value 0.5238 0.1299 0.6274
BSPLINE_best_roc_f1 0.7539 0.7282 0.9291
BSPLINE_best_roc_precision 0.7051 0.8902 0.9452
BSPLINE_best_roc_recall 0.8099 0.6161 0.9136
BSPLINE_best_roc_specificity 0.7139 0.5138 0.7139

Unanimity Vote

Name 0 - 0.5 0.5 - 1 0 - 1
RNA_best_roc_value 0.4932 0.2401 0.6398
RNA_best_roc_f1 0.7042 0.9010 0.9542
RNA_best_roc_precision 0.5797 0.9441 0.9586
RNA_best_roc_recall 0.8968 0.8616 0.9498
RNA_best_roc_specificity 0.5963 0.3785 0.6901
ED_best_roc_value 0.3432 0.2364 0.4305
ED_best_roc_f1 0.6509 0.6859 0.8123
ED_best_roc_precision 0.4902 0.9562 0.9506
ED_best_roc_recall 0.9684 0.5347 0.7092
ED_best_roc_specificity 0.3748 0.7017 0.7214
CBD_best_roc_value 0.3432 0.2409 0.4788
CBD_best_roc_f1 0.6519 0.7080 0.8582
CBD_best_roc_precision 0.4889 0.9552 0.9512
CBD_best_roc_recall 0.9779 0.5625 0.7818
CBD_best_roc_specificity 0.3653 0.6784 0.6970
CORR_best_roc_value 0.4157 0.0918 0.4522
CORR_best_roc_f1 0.6586 0.3240 0.8638
CORR_best_roc_precision 0.5721 0.9584 0.9461
CORR_best_roc_recall 0.7758 0.1950 0.7947
CORR_best_roc_specificity 0.6399 0.8968 0.6575
LA_best_roc_value 0.5660 0.2031 0.6579
LA_best_roc_f1 0.7394 0.8600 0.9590
LA_best_roc_precision 0.6094 0.9425 0.9602
LA_best_roc_recall 0.9401 0.7907 0.9578
LA_best_roc_specificity 0.6260 0.4124 0.7001
SIAM_best_roc_value 0.7386 0.1799 0.8243
SIAM_best_roc_f1 0.8315 0.7476 0.9720
SIAM_best_roc_precision 0.7566 0.9450 0.9813
SIAM_best_roc_recall 0.9229 0.6184 0.9629
SIAM_best_roc_specificity 0.8157 0.5615 0.8614
BSPLINE_best_roc_value 0.6629 0.0774 0.7106
BSPLINE_best_roc_f1 0.7903 0.4070 0.9422
BSPLINE_best_roc_precision 0.7410 0.9455 0.9713
BSPLINE_best_roc_recall 0.8465 0.2593 0.9147
BSPLINE_best_roc_specificity 0.8163 0.8181 0.7959

Case study using Impro-Visor

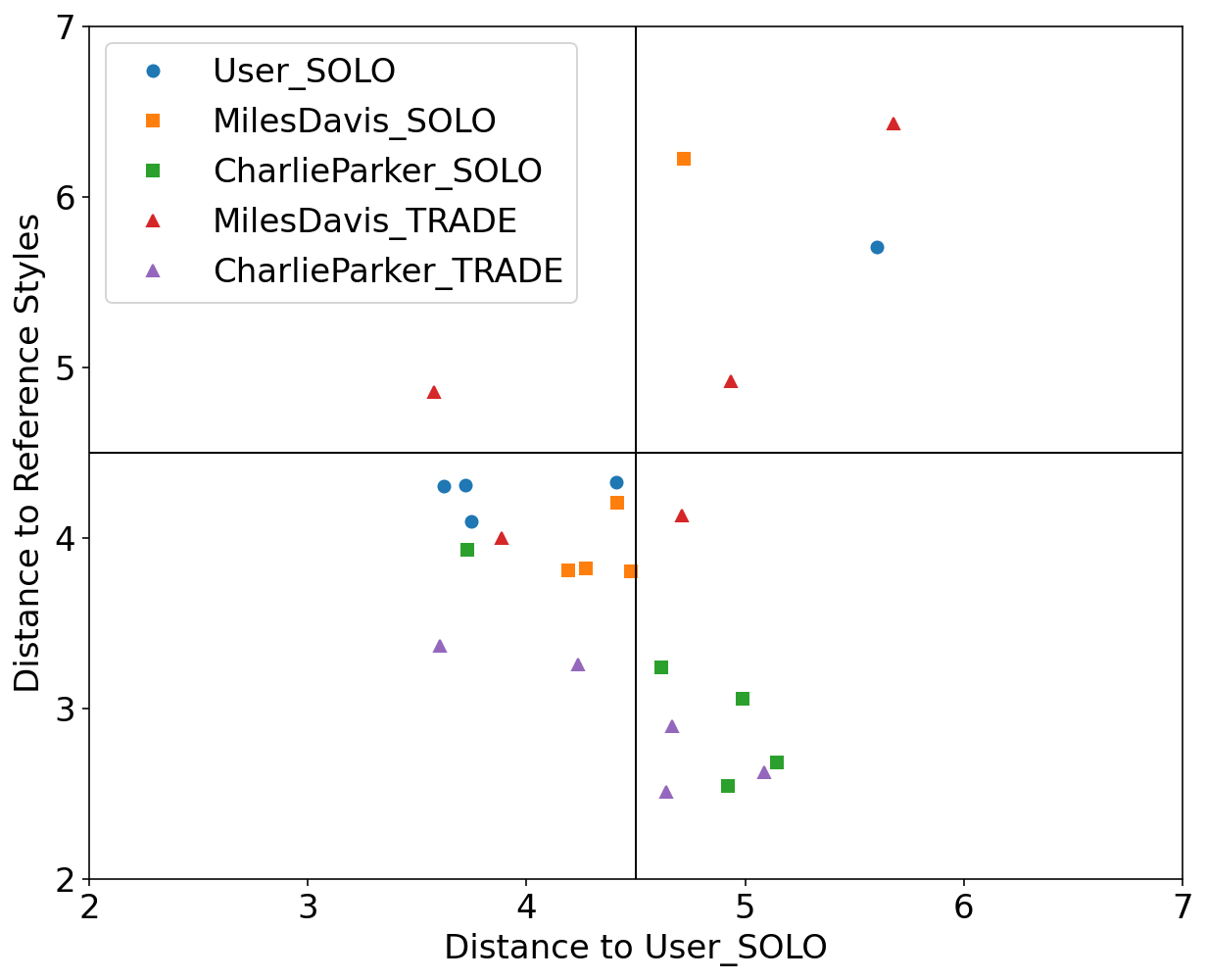
We used Impro-Visor to test the similarity measures that had the best results in our controlled experiments and for comparison is included a simple measure that is Euclidean Distance. For each group of melodies the similarity was calculated for the X axis to the Corpus created by the user. For the Y axis it was calculated with the corresponding solos of the composer pre-built grammar. For example the Tradings between User and Miles Davis were compared with User’s corpus for the X axis and with the grammar solos of Miles Davis for the Y axis.

The following melodies were used:

Corpus - User

Original pieces composed by an User, they are 12 measures in length.

Grammar Solo - Miles Davis

Using the pre-built grammar for Miles Davis in Impro-Visor, 5 melodies of similar length of 12 measures were generated.

Grammar Solo - Charlie Parker

Using the pre-built grammar for Charlie Parker in Impro-Visor, 5 melodies of similar length of 12 measures were generated.

Trading - User & Charlie Parker

With an active trade using 2 measures for each turn for a total of 12 measures, the User was asked to improvise using the prebuilt grammar of Charlie Parker.

Trading - User & Miles Davis

With an active trade using 2 measures for each turn for a total of 12 measures, the user was asked to improvise using the prebuilt grammar of Miles Davis.

Results

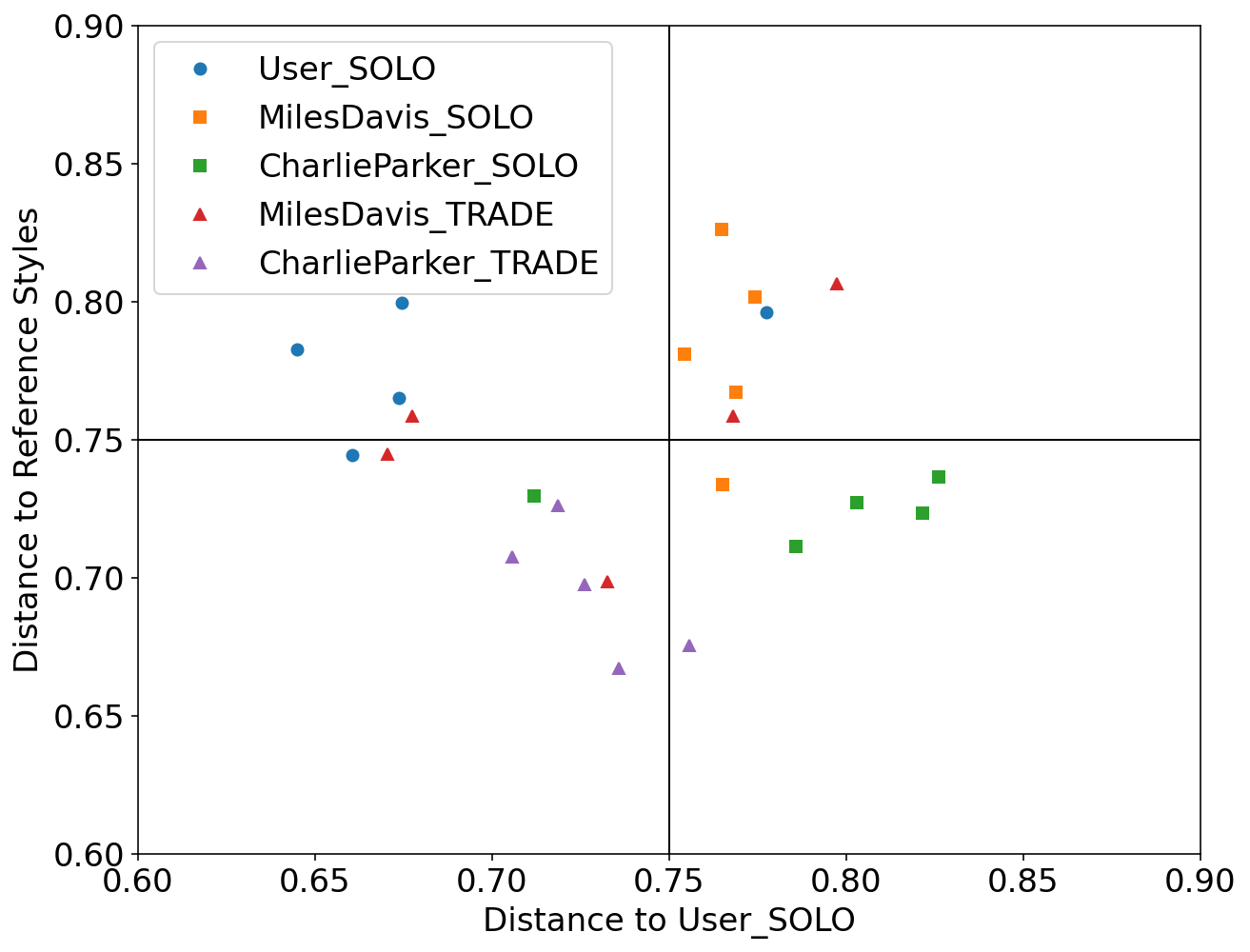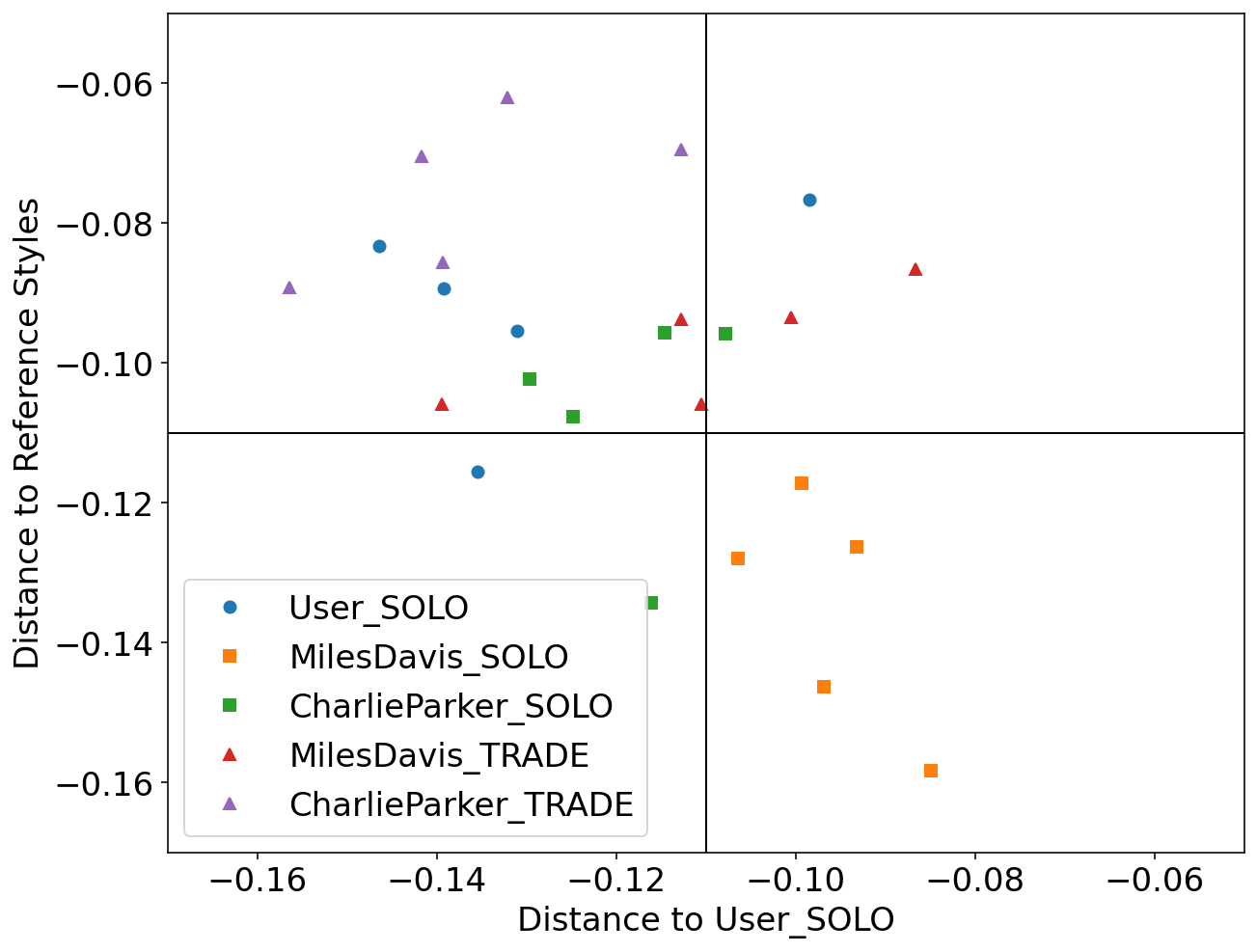RNA: Image SIAM: Image Local Alignment: 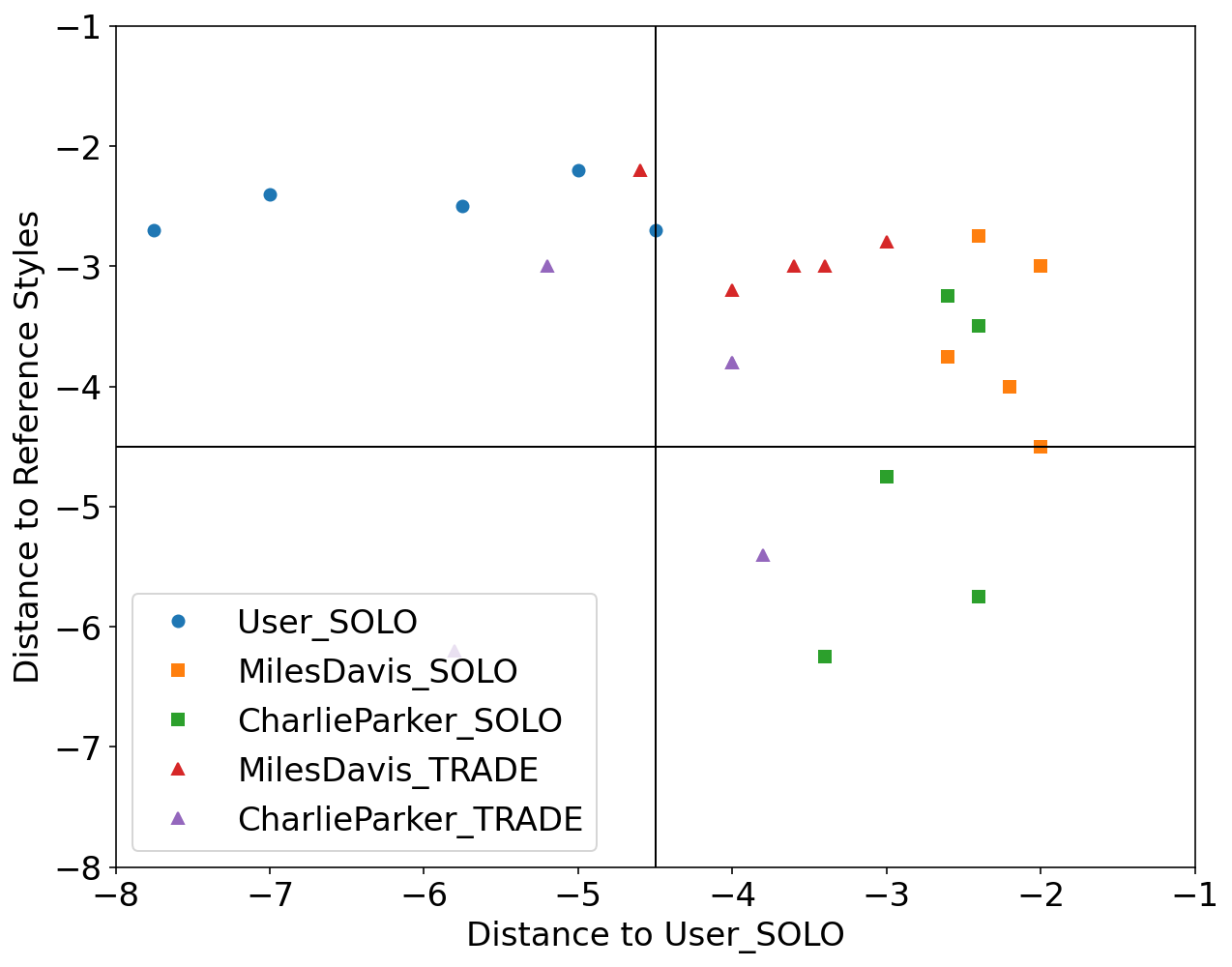Image Euclidean Distance: Image

The corresponding Jupyter notebooks can be found in this respository following this link.